PhoG: Sub-Poissonian Photon Gun

Fig. 1: A PhoG device (Photon-Gun) generates bright photon-number squeezed states via engineered dissipation and nonlinearity.

Project PhoG (Sub-Poissonian Photon Gun by Coherent Diffusive Photonics) develops a family of unique devices for generation of quantum states of light, a tailored light with user-selected properties. PhoG devices are based on engineered nonlinear loss in dissipatively-coupled optical waveguide networks, with the "cheap" attenuated coherent states as input. The nonlinear loss acts over much faster timescales than conventional (linear) loss, and so the system is robust to realistic physical limitations. In different regimes, PhoG acts either as a deterministic source of highly sub-Poissonian light, or as a source of entangled photons in different state configurations. Such wide performance range is enabled by a unique physical mechanism behind PhoG and by unique capabilities of the ultrafast laser inscription techniques. The strength of this approach is the ability to inscribe arbitrary patterns of 3-dimensional waveguide structures to create a desired configuration. The devices are compact, on a glass chip. Modern technologies widely use such integrated platforms which renders PhoG highly compatible with current technological systems.

Such quantum sources PhoGs (Photon Guns) will enhance the performance of many protocols across the Quantum Technologies arena by providing a ready alternative to attenuated quantum coherent states which are normally used because of their convenience. Within the project, we implement these devices to enhance super-resolution imaging and to improve stability of the commercial atomic clock. We will create proof-of-principle demonstrations of these applications. For the characterisation purposes, we have developed a unique detector, that can resolve large photon numbers and is based on the established concept of time-multiplexing, which was pioneered by members of the consortium.

The test board and the algorithms have been developed for the application of PhoG in super-resolution microscopy. Laser light passing through a quantum network of PhoG is transformed into special, entangled states of light. This allows to highly enhance the image quality using spatiotemporal quantum correlations. Apart from the purely quantum realm, our coherent devices can have classical applications, be used in quantum-inspired technologies, which perform better than standard classical devices. They will enrich integrated quantum photonics with devices in unusual operational regimes and can be generalised to other photonic integrated circuits (PIC) platforms.

In terms of societal applications beyond quantum realm, PhoG will contribute to the development of complex, custom designed 3 dimensional waveguide components that can be quickly changed and prototyped. It will advance on a new level the use of mid-infrared transmissive, high refractive index non-linear materials. This is particular important for biological applications, as mid-infrared sources and detectors allow access to the "fingerprint" region where compounds and molecules have distinct spectra allowing them to be identified. Custom light guiding components, spectrographs and lens arrays for the mid-infrared can be developed for minimally invasive portable detectors for precise and rapid clinical diagnosis and identification of diseases. For astronomical applications, integrated high precision, low loss spectrographs for the mid-infrared can be produced, which when used with ground- based telescopes operating with adaptive optics have the potential to identify and characterise Earth-like planets with the possibility to search for those capable of supporting life. Though not explicitly within the scope of the PhoG project, these PhoG-related advances of techniques and the expertise of partners contributes to further progress in all these applications.

Text taken from https://www.st-andrews.ac.uk/physics-astronomy/news/title-97703-en.php

Quantum Digital Signatures using homodyne measurements

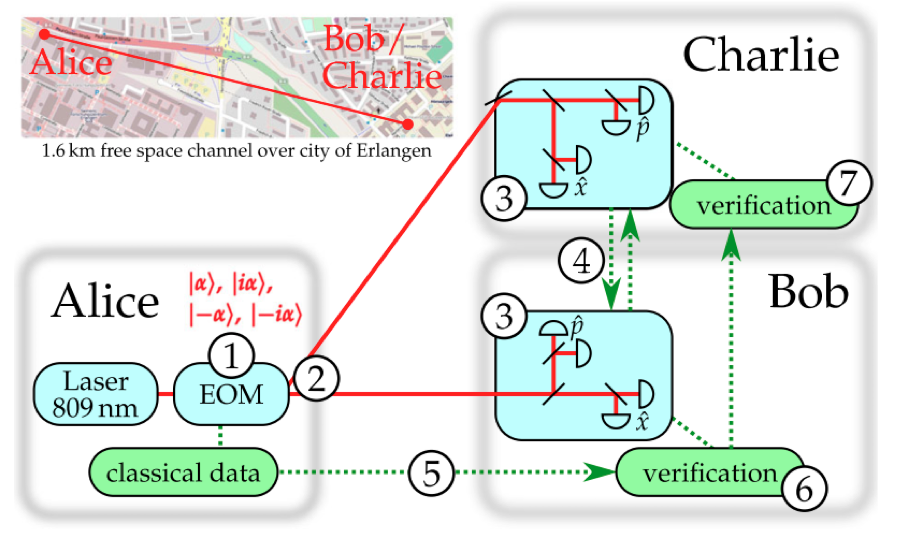
Digital Signatures [1-2] are widely used in today's digital communications to ensure the security and of messages. A digital signature should prevent a message from being forged or changed. Digital signatures should also prevent repudiation; a malevolent party should not be able to deny having sent a message which this party did actually send. Currently used classical digital signature schemes such as RSA, DSA and ECDSA, rely on the computational complexity of certain mathematical tasks, and will become insecure with the advent of quantum computing. For example, breaking the RSA signature scheme involves finding prime factors of large numbers. This task is currently difficult, but it is known to be achievable on a quantum computer [3]. We therefore seek an unconditionally secure signature scheme which will be secure even against arbitrary quantum attacks, with security based on information-theoretic grounds.

Fig. 1 Coherent state of light.

Quantum mechanics offers a promising setting for building secure signature schemes. Instead of basing a scheme on the assumed complexity of certain mathematical problems, security is based on physical law, in this case the inability to perfectly distinguish between non-orthogonal quantum states.

We are particularly interested in continuous variable (CV) signature schemes using non-orthogonal coherent states of light. In Fig. 1 a coherent state of light, |α⟩, is shown in phase space. The Gaussian tails of these states means they are not orthogonal to each other, allowing them to be used in quantum security protocols. We typically choose |α| to be small to limit the ability to forge a message.

A recent scheme [4] was proposed and implemented (Fig. 2 and 3), demonstrating that a CV QDS scheme can be highly efficient. Furthermore, coherent states are highly compatible with current telecommunication technology and infrastructure, making them a promising avenue of research into quantum security.

Fig. 2 Continuous variable QDS scheme.
Coherent states of light are generated at Alice and distributed to receivers Bob and Charlie. Bob and Charlie's measurement results can later be used to sign a classical message. Red: Quantum channels; Green: Classical channels.
Insert: experimental implementation of the scheme over a free space urban communication link of 1.6 km. Figure taken from [4].

Fig. 3 Free-space quantum communication set-up at the Max Planck Institute for the Science of Light, Erlangen, Germany, used in the CV QDS experiment [4]. Here Bettina Heim and Christoph Peuntinger prepare the receiver Bob, which is located in the computer science building at Friedrich-Alexander University Erlangen-Nuremberg.
Figure taken from the Max Planck Society Research magazine, Feb 2015.

Holographic quantum error-correcting codes for CV systems

Recent work has uncovered a deep connection between quantum error correction and the holographic principle [1]. The former is our attempt to protect quantum information from unwanted interactions with its environment. Whilst the latter states that there is an exact duality between systems of quantum gravity and quantum systems which lack gravity (but in a lower spatial dimension).
This link has given rise to a new interpretation: the mapping between these two dual systems is actually an error correction! This is because arbitrary operations (i.e. errors) may occur in parts of the purely quantum system, yet a perfect description of the quantum gravitational system can still be reconstructed.

Illustration of the holographic pentagon code. Picture taken from [1].

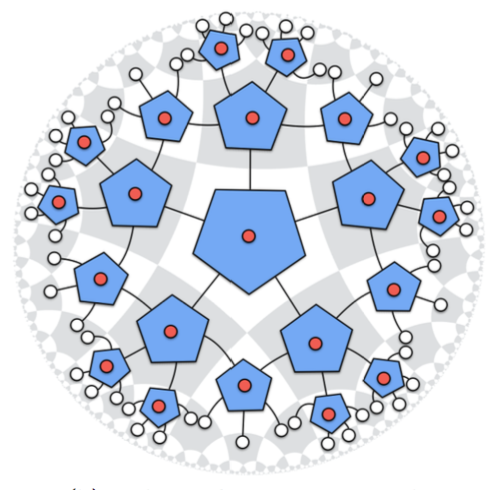
This project therefore focuses on so-called 'holographic codes', which are quantum error correcting codes that act as toy models of holography [1]. More specifically, the project attempts to develop a continuous variable (CV) holographic code, where the classic CV system is that of modes of the electromagnetic field (although many other examples exist, such as Bose-Einstein condensates). In other words, this would be an extension to the regime of optics.

This research therefore has the potential to not only develop better CV quantum error correcting codes, but may also shed some light on fundamental properties of physical CV systems such as finite squeezing.

Quantum tomography by noise and imperfections

Ultimately, the quantum tomography is the most comprehensive tool available for a researcher [1]. Indeed, by inferring the quantum state we have a possibility to predict results of any possible measurement. From its birth in 1989, quantum tomography has made an enormous progress. Now even such fragile quantum objects as "Schrödinger cats" made of photons are diagnosed and reconstructed. However, the most precise tool requires the most precise tuning. Generally, the quantum reconstruction schemes require precise calibration of the measurement set-up together with minimization of noise and losses. For example, one of the most established tomographic tools for electromagnetic field states, the quantum homodyne tomography requires more than 50% overall detection efficiency. Therefore there is quest for new, robust and user-friendly, tomography methods.

In view of this, we are looking for a possibility to exploit noise and imperfections as diagnostic tools. We have demonstrated both theoretically and experimentally [2] that reconstruction by noise is indeed feasible and provides a lucid, robust tomographic tool. By merely mixing the signal with the thermal noise and measuring the statistics of the resulting field on the on-off detector, we can collect data sufficient for inferring photon-number distributions of different signal fields.

Spectrally filtered light from such incoherent sources as an incandescent lamp can be used for the probe.

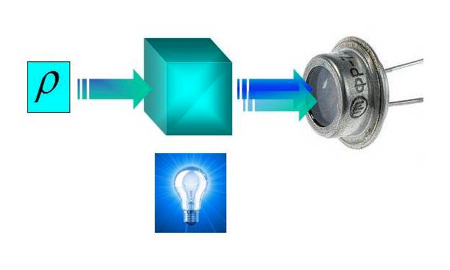
Our reconstruction scheme requires only a minimum number of precalibrated devices operating on the single-photon level. For collecting data, only a single on-off detector and a fixed ratio beam splitter were used. The reference field (thermal light) was calibrated using the same detector. Reconstruction of single-photon, thermal, and two-photon states was performed. The scheme has proven to be quite robust with respect to the noise and deviation affecting the measurement setup. Our scheme can be generalized to a complete tomography by adding coherent shifts to the signal. Potentially, even spectrally filtered light from such incoherent sources as an incandescent lamp can be used for the probe (see figure to the left).

Further we want to explore how non-ideal distinguishability between wave-packets can be used to perform a complete reconstruction of an unknown quantum state. Ultimately, the goal is to realize in practice for the first time the complete program of quantum diagnostics including self-calibration of the measurement set-up, checking for systematic errors and clarification of their nature. Processing of information with precision on the single-particle level or with efficiency beyond conventional standards requires extremely well-tuned diagnostics tools. We aim to demonstrate the feasibility of a complete control over a quantum measurement apparatus, self-calibrating and analysing it in the process of tomographic measurement itself.

The experiments related to these theoretical proposals are performed in the group of Prof. Ch. Silberhorn at the University of Paderborn, Germany.

Quantum correlations and entanglement

Quantum information science carries the potential for radically new means of computation, communication and information processing through the use of novel devices exploiting the laws of quantum mechanics. Coherence is a key notion here, being the underlying fundamental resource for all quantum information technologies. For instance, computational speed-up in the quantum realm comes from parallelism that stems from quantum coherent superposition states. Furthermore, all entanglement-enabled technologies in information processing and high precision measurement are emerging from coherence in its most general meaning, that is, from the correlations between physical quantities of quantum systems, from single quanta to optical modes, and their ability to interfere in a deterministic manner. However, it is not yet well understood how quantum correlations, or ultimately coherence, impacts on the computational performance and complexity of tasks that can be implemented and how to efficiently protect such systems from the environment. Studying decoherence and noise effects in combination with coherence and correlations will provide vital insights for radically new technologies.

Gaussian entanglement. Quantum correlations and quantum discord. Multipartite quantum communication protocols

For our full research scope on this subject see publication list below. Here we highlight two recent experiments demonstrating several tri-partite quantum communication protocols. We briefly describe the fascinating physics of quantum correlation which underlies these protocols. The notable feature of these protocols is that they all are based on realistic, noise quantum mixed states.

1   Entanglement distribution by separable ancilla

In [7], we experimentally demonstrate the entanglement distribution by a separable ancilla [T. S. Cubitt, F. Verstraete and J. I. Cirac, "Separable states can be used to distribute entanglement", Phys. Rev. Lett. 91, 037902 (2003).] with Gaussian states of light modes [1,2] (Fig. 1). The protocol aims at entangling mode A which is in possession of a sender Alice with mode B held by a distant receiver Bob by local operations and transmission of a separable mediating mode C from Alice to Bob. This requires the parties to initiate their modes to a specific correlated but fully separable Gaussian state. Once the resource state ABC is established no further classical communication is needed to accomplish the protocol.

Fig. 1   Entanglement distribution by separable ancilla [1,2,7] – correlated noise creates coherence!

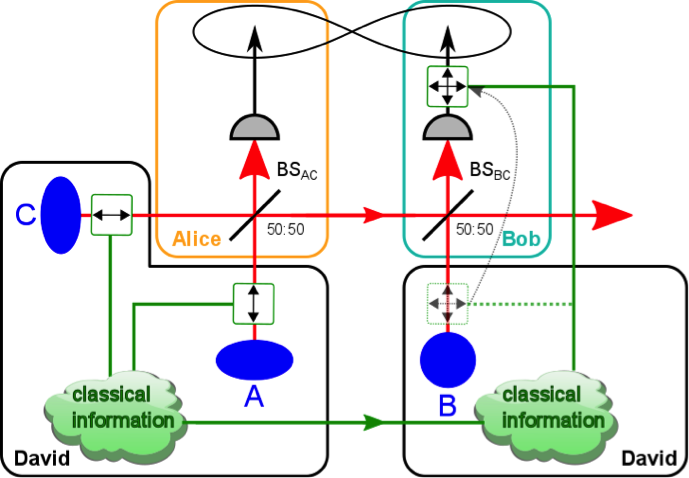
To emphasis this, we attribute the state preparation process to a separate party, David. Note, that this resource state preparation is performed by LOCC only. No non-local, global quantum operations are executed at the initial stage and no entanglement is present. It is remarkable that the creation of entanglement between two observers can be disassembled into local operation and communication of a separable quantum system between them. Impossibility of entanglement creation by LOCC is not violated here because communication of a quantum system is involved. The corresponding protocol exists only in a mixed-state scenario and obviously utilizes less quantum resources in comparison with the previous cases because communication of only a discordant separable quantum system is required.

2   Entangling power of a beamsplitter

A beamsplitter (BS) is frequently used to generate entangled continuous variable states, if at least one of the inputs is a quantum squeezed state. BS is passive and can only create entanglement if there is some quantumness initially. At the example of several protocols [7-10], we have demonstrated experimentally, that for mixed quantum states, a BS can create entanglement even from two input modes none of which exhibit any local squeezing, provided that they are correlated in a tailored way with a third one (Fig. 2). These correlations are quantified by Gaussian quantum discord. We have demonstrated the entangling power of a BS with discordant correlations as a resource with three multi-partite protocols.

Fig. 2   Entangling the whole by beam splitting a part. [10]

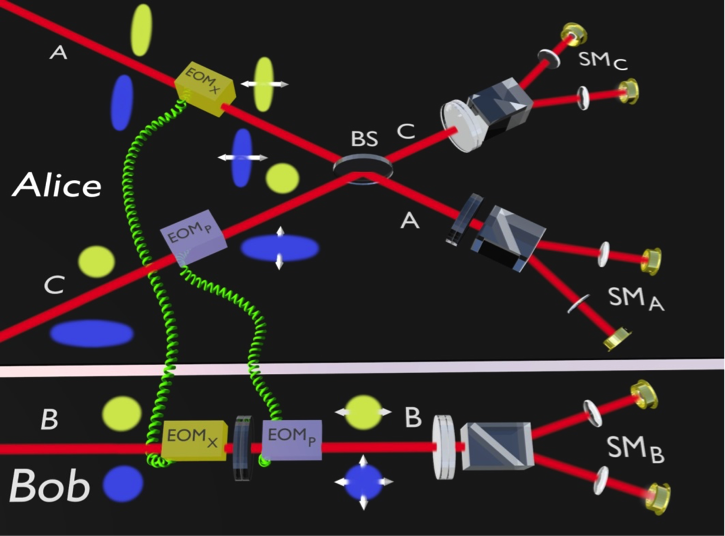
(1) This mechanism is behind the entanglement distribution by separable ancilla [1,2,7] discussed above. In this protocol, two modes A and B and the ancilla C are initially in a three-partite fully separable state. After C interference on a BS first with A and then with B, A and B become entangled. C remains separable throughout the protocol. The initial state ABC is though separable but discordant, that is, all three modes are correlated in a particular fashion.
(2) It enables the recovery of entanglement from the noise-affected squeezed states via interference with a correlated "environmental" mode [9].
(3) It allows for generation of a three-partite entangled state by splitting on a BS a thermal state correlated with a vacuum mode [10]. In this latter protocol the created entanglement does not occur between the output modes of the BS but instead it emerges between one output mode and the remaining two modes taken together. This phenomenon is a key element of the protocols for entanglement distribution with separable states above [7], and for entanglement sharing.

Dissipation protects and creates quantum coherence

The noise properties, in particular correlated and coherent noise, and the coupling to the environment in general, represent an as yet not sufficiently explored and exploited mechanism for coherent signal transport and system control. Some properties of the correlated noise and interaction with environment have been exploited in the communication protocols described above. Here we look at a wider scope of problems which include engineered dissipation and dissipation to a common reservoir as an effective tool to maintain or even create quantum coherence.

Selected past topics