Bose condensation of Excitons and Polaritons
The following is an extract discussing the general idea of quantum-mechanical coherence, as it may be observed in Bose-Einstein condensation, and introducing the excitons and polaritons as candidate systems. There is also a list of references, and of other resources.
The general object of my research is the study of systems for which the predictions of quantum mechanics differ significantly from those of classical mechanics. To make this statement less gnomic it is necessary first to understand why, in many circumstances, systems which can always be described by quantum mechanics, can also be adequately described by classical physics.

Young's slits, showing interference pattern due to various paths through slits.
Many of the strange aspects of quantum mechanics can be understood by
considering the famous two-slit experiment
[Young 02],[Young 03].
If light of a single frequency is shone on a screen containing two
closely spaced slits, this light will then create a series of
fringes on a screen placed beyond the slits.
This can be explained classically; light is an electromagnetic
wave, and so the light going through the two slits can
interfere constructively — producing a bright fringe, or
destructively — producing a dark fringe.
The pattern reflects the relationship between the phases
of the waves travelling via two different paths.
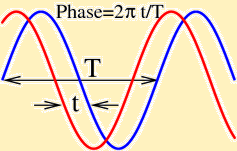
[Note:
The phase difference between two waves can be understood as the
delay between the peak of one wave and the other, as a fraction of
the total period of a wave. If the phase difference is zero, or an
integer in this language, then the waves are in phase, their peaks
align. If it is π
then the peaks of one align with the troughs
of the other, they are out of phase.
 ]
]
However, from other experiments, one can show that light comes in isolated ``quanta'', known as photons. For light of a given wavelength, there is a smallest unit of energy that can be transferred. If one repeats the two-slit experiment at low intensities, one can be sure that, at any time, at most one quantum of light exists in the apparatus. The pattern remains. Further, the same pattern can be seen for single electrons, for atoms, for cold clouds of many atoms or for large molecules.
In all these cases, if one argues that the photons, atoms or electrons behave as particles, then each particle must pass simultaneously through both slits; this is what quantum mechanics describes. The behaviour of a particle is governed by its wave-function, a function of its coordinates, which when squared gives the probability of finding the particle at such a position. Interference between the wave-function for particles coming through one slit and the other is responsible for the fringes observed.
This behaviour, which requires the introduction of quantum mechanics is however normally only seen on the microscopic scale, for various reasons: Firstly, the heavier the object, the closer the interference fringes, and so the harder it becomes to observe them. More importantly, for the fringes to persist, it is necessary that one cannot determine through which slit the particle went. With large objects it becomes increasingly hard to prevent such information being observed. Interactions between the system and the environment will change the quantum state of the system.
There exist a variety of systems which, despite these problems, can show quantum mechanical behaviour on macroscopic scales. A common feature of many of these systems is a phase transition to a ``coherent state''. Phase transitions, such as the freezing of a liquid, or the change of magnetic properties of some metals on cooling, are associated with a change of symmetry — a solid has a periodic structure, and so is no longer symmetric under translations; a permanent magnet has a direction of magnetisation and is no longer symmetric under rotations. In a transition to a coherent state, the symmetry that is broken is associated with the phase of the quantum wave-function [Anderson72].

Image of a ``Superconducting Quantum Interference Device'': The current-voltage characteristics depend on the magnetic flux through the loop in the superconducting wire (the hole in the middle) [Image From: Berkely Lab website.]
Examples of such coherent states include superconductivity (as described by Bardeen, Cooper and Schrieffer, referred to as BCS from here) [Bardeen, Cooper, Schrieffer 72], superfluid helium [Landau62], Bose-Einstein Condensation (BEC) of dilute atomic gases [Cornell, Ketterle, Wiemann 01], and recently experiments on excitations of semiconductor systems (which I shall discuss later). As an example of the analogue of the two-slit experiment in such systems I mention ``Superconducting Quantum Interference Devices'' (SQUIDs) which are routinely used to measure small magnetic fields. A magnetic field can change the phase of electrically charged particles, in such a way that the interference of superconducting currents flowing in opposite directions around small metal rings can measure to high accuracy the magnetic field there.
Before discussing further what is a coherent state, it is necessary to point out another feature of quantum mechanics. If one considers identical particles, one can ask what happens to their wave-function if they are exchanged. As they are identical, the probability of the two configurations, given by the square of the wave-function, must be the same; but this could allow the wave-function to be multiplied by -1, without changing the probability. All types of particle can be classified by whether this exchange gives +1 or -1. If one considers pairs of particles, the factors multiply.
If the answer is -1, then there can be no probability of finding two such particles in the same place: The wave-function for two particles being at the same place is equal to itself multiplied by -1, this implies it must be zero. This category of particles are called fermions, after Enrico Fermi. This include electrons, protons, neutrons, and some atoms (depending how many electrons, protons and neutrons they contain -- the number must be odd). The other category is bosons, named after Satyendra Bose, and includes photons, alpha particles, excitons, polaritons, and those atoms with even numbers of electrons, protons and neutrons.
For the same reasons that light comes in quantised units of energy, excited states of a system have quantised energies. At zero temperature, a system will be found in the lowest possible energy state. If the system consists of bosons, this state will generally have all particles with exactly the same wave-function. One can then ask how extra energy can be added to the system.
In a finite system, there will be a smallest amount of energy that can be added; a finite gap to the first excited state. For temperatures lower than this, the system will always be coherent. This is not BEC; for any macroscopic system such a temperature would be infeasibly small. For interacting systems, one may instead find a transition that occurs at much higher temperatures, driven by the interactions between particles.
The particular systems with which my work has been concerned are ``quasi-particles'' in semiconductors. When considering large numbers of interacting particles, it is often more illuminating to discuss the collective motion of many particles in terms of weakly interacting quasi-particles. In many problems, the effort of identifying the combination of elementary particles which form a quasi-particle is equivalent to solving the entire problem.
For instance, electrons moving through a semiconductor crystal interact strongly with each other, and with the atoms forming the crystal lattice. The latter can be described by the motion of a quasi-particle, with similar properties to the electron, but a different effective mass. Under certain conditions these quasi-particle may have a negative mass; i.e. when a force is applied in one direction, it moves in the other — this is a result of attempting to describe all interactions with the lattice by an effective mass. Under these conditions, one can more easily consider the behaviour of a missing electron, a hole, which will have a positive mass, and the opposite charge.
Including the effects of interactions between different electrons in the lattice can, in some materials, lead to the formation of neutral particles known as ``excitons''. These occur when a material contains a small number of electrons and also of holes. Such a system can occur when a semiconductor is illuminated with light of a certain wavelength. This will take electrons at an energy where they would have had negative mass, and excite them to a regime where they have positive mass; the result is free electrons and free holes in the same sample. These can attract each other and form a bound pair, analogous to a hydrogen atom, but with a much smaller mass.
However, such particles have a finite lifetime; since they can be created by shining light on the material, they can recombine and release their energy as light. In certain materials this process is slow, and it then becomes possible to perform experiments on excitons.
These excitons, at least at low densities, behave similarly to the atoms that form a BEC. However, they are far lighter; their mass is at least ten thousand times less than that of a sodium atom. The temperature at which bosons condense is governed by the inverse of the mass, so the temperatures required for exciton condensates may be of the order of a few tenths of a degree above absolute zero, rather than the millionth of a degree above absolute zero required for atomic gases.
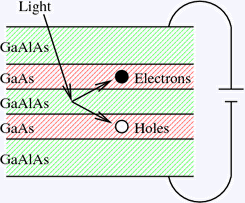
Diagram of excitons in double quantum-well systems; due to an applied voltage, electrons and holes are confined to separate layers of semiconductor (labelled GaAs — Gallium Arsenide).
Although there has been thirty years work on related systems, there is as yet no conclusive evidence for BEC of excitons. However, in recent years an engineered semiconductor system has been considered, in which the electrons and holes are made to occupy different regions of space, while remaining close enough to interact. In these systems, recent experiments [Butov 02 (a)], [Butov 02 (b)] [Negoita 02], show hints of condensation.
Taking this argument further, one would like to form bosons with yet smaller masses; but at the same time one needs to be able to trap and cool them. The quanta of light, photons, have strictly zero mass, but interact weakly, and are hard to confine, so alone one can not form a condensate. However, placing a semiconductor sample between two high quality mirrors, one can construct a system containing ``polaritons'' in a ``microcavity''. Polaritons are the quasi-particles that result from considering excitons turning into photons, and turning back into excitons again. As suggested above, by this change of language, one describes a quasi-particle that includes all such repeated processes, and finds new properties for such particles.
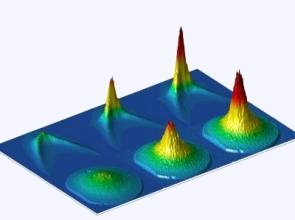
Occupation of different energy/momentum states across the condensation threshold for microcavity polaritons: left-most case is uncondensed, right-most is condensed. The further set of images show occupation versus energy and momentum, the nearer show occupation versus two components of momentum. [From J. Kasprzak, adapted from [Kasprzak 06]]
Polaritons have yet smaller masses, some thousand times less than excitons, and so one could conceive of condensation at a temperature of a few degrees above absolute zero. Experimental progress over the last decade [LeSi 98] [Deng 02] [Deng 03], [Weihs 04], has been substantial, and a recent, and comprehensive set of experiments [Kasprzak 06], have clearly demonstrated long range spatial and temporal coherence, along with macroscopic occupation of the lowest energy modes, in a non-resonantly pumped system which — crucially — remains well thermalised as coherence appears.
In such systems, one has access to two important general areas of physics which contain unanswered questions. One is the condensation of quasi-particles which are weakly bound, i.e. for which it is easy to break up the quasi-particle. [Note: Even for an atomic gas, the atoms are quasi-particles, consisting of interacting electrons, protons, neutrons etc.; however excitations which probe this structure need very high energy. This is why it was not till the early twentieth century that energies sufficiently high to probe atomic structure were available. ] This applies to excitons at high densities, to polaritons at intermediate densities, as discussed below, and also recently to experiments involving tunable interactions between cold atoms. The second area, which is the subject of several proposed items of research, is the study of macroscopic quantum coherence in systems with short lived particles, which necessarily will be out of thermal equilibrium.
To conclude this introduction where it started, I mention briefly very recent results of experiments with polaritons driven by a coherent light source, i.e. by a laser. These experiments differ from those with which my work is mostly concerned, as here the coherence is a result of the input to the system, not spontaneous. However, in such systems, one can again perform a version of the two-slit experiment, with interference fringes which vanish when one could record which way a polariton went.
References
- [Young 02] T. Young. On the theory of light and colours Phil. Proc. Roy. Soc. 92 12 (1802)
- [Young 03] T. Young. Experiments and calculations relative to physical optics Phil. Proc. Roy. Soc. 94 1 (1803)
- [Anderson 72] P. W. Anderson More is different Science 177 393 (1972)
- [Bardeen, Cooper, Schrieffer 72] J. Bardeen and L. Cooper and J. Schrieffer, Nobel Lecture (Superconductivity), (1972). (Nobel website (1972))
- [Landau 62] L. Landau Nobel Lecture (Superfluidity), (1962) (Nobel website (1962))
- [Cornell, Ketterle, Wiemann 01] E. Cornell and W. Ketterle and C. Wiemann} Nobel Lecture (Bose Einstein Condensation of Dilute atomic Gases), (1962) (Nobel website (2001))
- [Butov 02 (a)] L. V. Butov, C. W. Lai, A. L. Ivanov, A. C. Gossard and D. S. Chemla Towards Bose Einstein Condensation of Excitons in potential traps Nature 417 47 (2002). (DOI: /10.1038/417047a)
- [Butov 02 (b)] L. V. Butov, A. C. Gossard and D. S. Chemla, Macroscopically ordered state in an exciton system Nature 418 751 (2002). (DOI: /10.1038/nature00943)
- [Negoita 02] V. Negoita, D. W. Snoke and K. Eberl Harmonic-potential traps for indirect excitons in coupled quantum wells Nature 418 754 (2002) (DOI: /10.1038/nature00940)
- [LeSi 98] Le Si Dang, D. Heger, R. André, F. Bœuf, and R. Romestain Stimulation of Polariton Photoluminescence in Semiconductor Microcavity Phys. Rev. Lett. 81 3920 (1998) (DOI: 10.1103/PhysRevLett.81.3920)
- [Deng 02] H. Deng, G. Weihs, C. Santori, J. Bloch and Y. Yamamoto Condensation of Semiconductor Microcavity Exciton Polaritons Science 298 199 (2002) (DOI: 10.1126/science.1074464)
- [Deng 03] H. Deng, G. Weihs, D. Snoke, J. Bloch and Y. Yamamoto Polariton lasing vs. photon lasing in a semiconductor microcavity Proc. Natl. Acad. Sci. 100 15318 (2003) (DOI: 10.1073/pnas.2634328100)
- [Weihs 04] G. Weihs, H. Deng, D. Snoke and Y. Yamamoto Polariton lasing in a microcavity Phys. Stat. Sol. 201 625 (2004) (DOI: 10.1002/pssa.200304061)
- [Kasprzak 06] J. Kasprzak, M. Richard, S. Kundermann, A. Baas, P. Jeambrun, J. M. J. Keeling, F. M. Marchetti, M. H. Szymanńska , R. André, J. L. Staehli, V. Savona, P. B. Littlewood, B. Deveaud and Le Si Dang Bose-Einstein condensation of exciton polaritons Nature. 443 409 (2006). (DOI: 10.1038/nature05131)
Other resources
- Bose Condensation in Atomic Systems
-
The following two sites are the groups of the researchers who were jointly awarded the Nobel prize for Bose Einstein condensation in 2001.
- BEC projects web page of Prof. Ketterle's group at MIT.
- BEC web page at the University of Colorado at Boulder.
- Bose condensation of Excitons in double quantum wells
- Exciton condensation at University of California at San Diego.
- Here is a link to slides from a talk I gave to my colleges scientific society on Bose Condensation of excitons
- Bose condensation of Microcavity Polaritons
- Microcavity polaritons at Stanford .
- Microcavity polaritons at University Joseph Fourier, Grenoble.

