In the first few parts of this set of pages we saw that the amount of information conveyed along a channel will depend upon its bandwidth (or response time), the maximum signal power, and the noise level. The way we estimated the effects of these was fairly rough. We now need to look at this fundamental question of a channel's information carrying Capacity more carefully. The amount of information contained in a message can be formally defined using the Sampling Theorem. The maximum information carrying capacity of a transmission channel can be defined using Shannon's Equation. Taken together, they provide the basis of the whole structure of Information Theory. Rather than tackle the Sampling Theorem or Shannon's Equation ‘head on’, it is useful to take a diversion and begin by considering the relationship between a time-varying signal and its Frequency Spectrum.
A message which requires an infinite time to finish isn't of any practical value. This is because we can't know what information it contains until it has all arrived! As a result, in practice we can only observe or deal with signals which have defined ‘start’ and ‘stop’ points. The fact that information about a real signal or process can only cover a finite duration or interval has some important consequences.
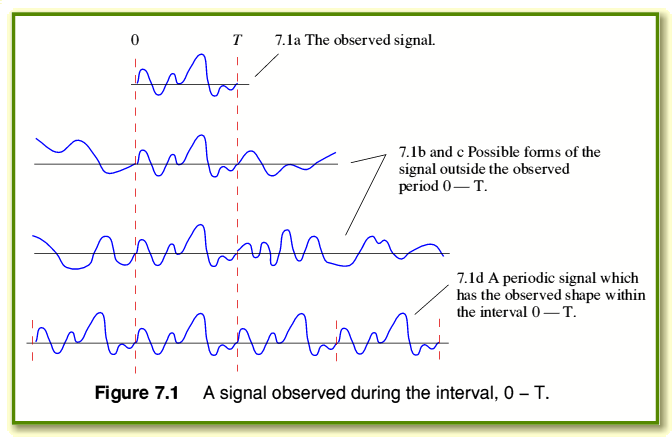
Consider the situation illustrated in figure 7.1a. This shows how a particular analog signal is seen to vary over a time interval, t = 0 to t = T. (For simplicity we've ‘switched on the clock’ at the start of the observation. Note that this doesn't affect our conclusions.) Now the only message information we have is confined to the chosen time interval. Logically, therefore, we have to accept that if we had looked at the signal for at other times we might have seen any of the alternatives shown in figure 7.1b, c, etc. However, the limited information we have doesn't allow us to know what happened outside our observation. We can, of course, theorise about what we might have seen if we had observed what was happening at other times. Provided any hypothesis doesn't conflict with the information we possess it can be accepted for the purpose of argument.
The signal we have observed can be described by some specific function of time, 
, which is only known when 
. From the argument given above we can, in principle, imagine an infinite variety of theoretical functions, 
, which are defined so that
but which allow 
to do whatever we like at other times.
Using functions like 
or 
we can describe the behaviour of a signal in terms of its variations with time. An alternative method for describing a signal is to specify its frequency spectrum in terms of some suitable function,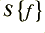 
. We can then consider the signal level at any instant, t, as
i.e. the signal is regarded as being composed of a series of contributions at a set of frequencies, 
. The size of each contribution, 
and its phase at t = 0, 
, being defined by the value of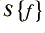 
at the appropriate frequency, 
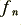. (Note that this means that, in general, 
must specify two values, an amplitude and a phase, hence it is most convenient to treat this as a function which produces a complex result.)
Clearly the time domain description,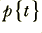 
, of a signal and its frequency domain description, 
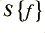, must contain identical information if they are both to specify the same signal or message. The two functions must therefore be linked in some way. Mathematically, this link can be made using the technique called Fourier Transformation.
Content and pages maintained by: Jim Lesurf (jcgl@st-and.ac.uk)
using HTMLEdit and TechWriter on a StrongARM powered RISCOS machine.
University of St. Andrews, St Andrews, Fife KY16 9SS, Scotland.
