Experience shows that it can be a mistake for a student to read more than one book which uses Fourier analysis! Comparing one text with another reveals a host of odd factors of 2, 
, etc., which seem to pop up and disappear without any obvious reason. The most common result of this is to make most engineering and science students decide to avoid the topic whenever possible! Unfortunately, Fourier methods are very useful. Ignoring them is a bit like avoiding using saws when doing woodwork because you aren't sure which type of saw is best. Since this isn't a maths book we won't examine Fourier Transforms in detail, but it is worth making a few comments which may be helpful.
Firstly, we can see from looking back at equation 7.2 that to specify the effect of a given frequency component on a signal we need to have two values. In 7.2. these were an amplitude, 
, and a phase, 
. We could, however, achieve the same effect in other ways. For example, we could define the same signal in terms of pairs of values,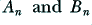 
, in an expression like
or we could use something like
All of these are equivalent ways to achieve the same result, but they alter the form of the Fourier Transform expressions required to link the time and frequency domains.
Secondly, the form of the Fourier Transform expressions depends upon whether we are interested in knowing the power (or amplitude) of the signal or the total energy it conveys. This affects whether the expressions have to be multiplied by a factor proportional to 
since power = energy per unit time. Here we will use the type of expression given in 7.3 and consider the amplitude (e.g. the voltage) of the signals. This determines the details of the Fourier Integrals we'll use. In fact, we would come to the same conclusions using any of the other approaches.
Sines and cosines are an example of a set of Orthogonal Functions. The general topic of the properties of orthogonal functions is beyond the scope of these pages. All we have to do is outline some of their basic properties which are relevant here. In general, a set of functions,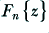 
, which satisfy the integral
are said to be ‘orthogonal over the range a to b’. For the case of sine or cosine functions we can regard 
and 
as having two different angular frequencies, 
, 
. If we consult a book of integrals or a text on the properties of functions we can find that, provided 
where m and n are integers. This is equivalent to saying
where 
. We can interpret this as defining a ‘fundamental frequency', 
, which can fit one half-cycle into the interval, T.
This orthogonal behaviour is very important for the usefulness of Fourier analysis. The reason for this can be understood by going back to the signal we considered at the start of the previous webpage. This is a signal, 
, whose value is known only during the interval, 
.
As we have seen, we can imagine a variety of functions, 
, which are identical to 
during this observed interval but behave however we wish at other times. Provided we always ensure that 
during the signal interval every possible choice of 
provides us with exactly the same information (pattern) during this period as 
. All these possible choices are indistinguishable from one another if we only observe this finite interval. This gives us the freedom to choose any 
which is identical to 
during the observed interval. We can therefore select one which is convenient for the purpose of analysing the signal. There is nothing to stop us from choosing a form for 
which is Periodic — i.e. one which repeats itself over and over again — with a period equal to the observed signal's interval, T. This assumption is convenient for the purposes of Fourier analysis. If we assume 
is periodic in this way it will take the form shown in figure 7.1d.
It should be clear that a signal which repeats itself in this way can only contain frequencies which are multiples of a fundamental frequency, 
(plus, perhaps, a non-zero d.c. level). This is because the presence of any other frequencies would mean each ‘cycle’ of the periodic function would differ from its neighbours. We can therefore say that the function must be of the form
where N represents the highest frequency present and the 
values determine the magnitude and phase of the n th frequency component of the signal. Note that this expression only contains a d.c. level (
, a component at the fundamental frequency, 
, and components at its harmonic frequencies, 
. (As 
and 
the d.c. level equals 
. 
has no physical meaning.) Since this function is chosen so as to be indistinguishable from 
during the observed period we can therefore say that 
is indistinguishable from
during the observed period. The coefficients, 
may be obtained from 
using the Fourier integrals,
These expressions represent the Fourier Transform of the known signal, 
, and allow us to calculate the signal's frequency spectrum. (Expressions 7.10 and 7.11 can be seen to be true once we accept that 7.6 and 7.7 are correct. In effect, the above expressions let us ‘pick out’ the two coefficients we want from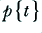 
at any chosen frequency, 
.)
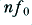From the above arguments it should be clear that we can freely convert information back and forth between the time domain and the frequency domain. Given this ability it must be true that the frequency spectrum contains the same information as the time-varying signal.
Content and pages maintained by: Jim Lesurf (jcgl@st-and.ac.uk)
using HTMLEdit and TechWriter on a StrongARM powered RISCOS machine.
University of St. Andrews, St Andrews, Fife KY16 9SS, Scotland.
